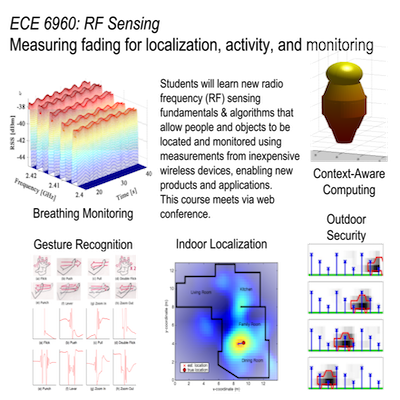
The Sensing and Processing Across Networks (SPAN) Lab at the University of Utah develops new technologies at the intersection of wireless networking, radio propagation, and signal processing. The SPAN Lab has been at the forefront of the development of the use of standard wireless devices for the purpose of monitoring the state of the environment, for example, for localization and tracking, breathing monitoring, and context awareness, and to provide increased reliability and security for wireless networks.